中間利息を控除するには、控除期間（年数）に対応するライプニッツ係数あるいはホフマン係数を使います。現価表と年金現価表があり、利用するシーンが異なります。
ライプニッツ係数表・ホフマン係数表をエクセルで簡単に作成する方法
ライプニッツ係数表・ホフマン係数表は、エクセルを使えば自分で簡単に作成することができます。セルの2ヵ所に計算式を設定して、あとはコピペするだけ。その方法をご紹介します。
※当サイトでは記事内にアフィリエイト広告を含む場合があります。
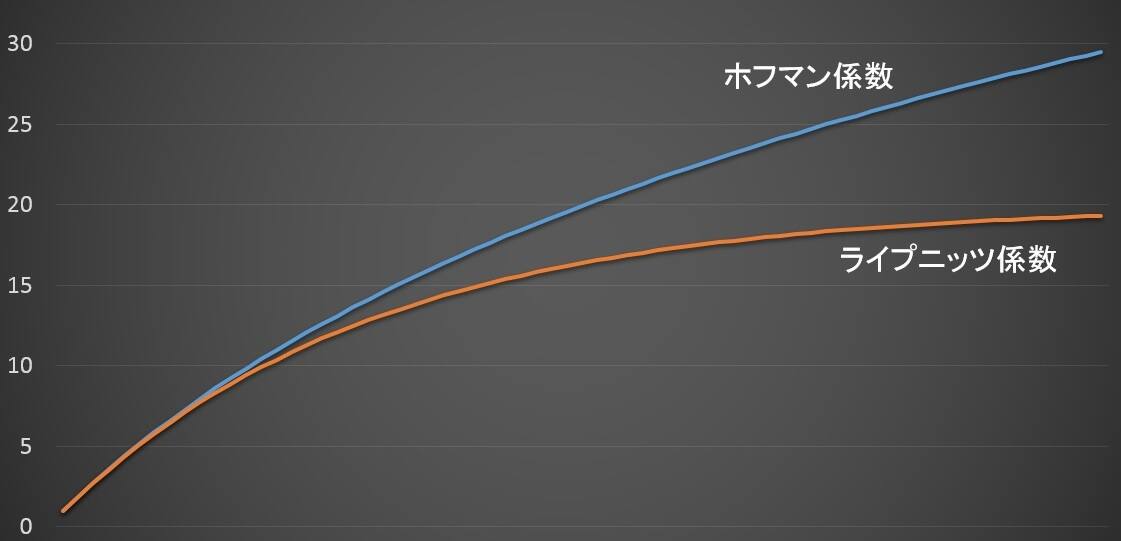
ライプニッツ係数表やホフマン係数表は、エクセルを使って簡単に作成できます。
ライプニッツ係数表・ホフマン係数表には、「現価表」と「年金現価表」があります。この2つの関係についても知っておく必要がありますから、まずは「現価表」と「年金現価表」の関係から説明します。
「現価表」と「年金現価表」の関係
給与等の逸失利益の計算には「年金現価表」を使い、退職金等の逸失利益の計算には「現価表」を使います。現価表と年金現価表が、どんなものか、それぞれどんな場合に使うか、詳しくはこちらをご覧ください。
それでは、「現価表」と「年金現価表」の関係について見ていきましょう。
「現価表」の係数を小文字のアルファベットで、「年金現価表」の係数を大文字のアルファベットで表すと、次のようになります。5年分だけ表にしています。
| 年 | 現価表の係数 | 年金現価表の係数 |
|---|---|---|
| 1 | a | A |
| 2 | b | B |
| 3 | c | C |
| 4 | d | D |
| 5 | e | E |
「現価表」の係数と「年金現価表」の係数との間には、次のような関係があります。
A＝a
B＝a＋b
C＝a＋b＋c
D＝a＋b＋c＋d
E＝a＋b＋c＋d＋e
「年金現価表」の係数は、「現価表」の係数を期間分（年数分）足し合わせたものです。ですから、「現価表」を作成できれば、1年目から期間分の係数を積算すると「年金現価表」を作成できます。
それでは、ライプニッツ係数表とホフマン係数表をエクセルを使って作成してみましょう。
ここでは年5％の法定利率のライプニッツ係数・ホフマン係数について説明しますが、民法改正により法定利率が引き下げられ、2020年4月1日以降に発生した事故については新しい法定利率に対応するライプニッツ係数・ホフマン係数が適用されます。
ホフマン係数表（現価表・年金現価表）をエクセルで作る
ホフマン方式は、単利で運用することを前提に、将来の逸失利益を現在の価額（現価）に換算する方法です。別の言い方をすれば、単利で運用した場合の運用利息（中間利息）を控除して現価を出す方式です。
r：利率（年利）
n：期間（中間利息を控除する期間・年）
P：現在の価額（現価＝元本＝逸失利益）
V：将来の価額（n 年後の価額）
1年後の金額
「元本」に「1年間の利息」を加えた金額ですから、
P＋Pr＝P(1＋r)
2年後の金額
「1年後の金額」と「この1年間の利息」を加えた金額です。単利ですから、利息は元本にのみ付きます。
P(1＋r)＋Pr＝P(1＋2r)
3年後の金額
「2年後の金額」と「この1年間の利息」を加えた金額ですから、
P(1＋2r)＋Pr＝P(1＋3r)
n 年後の金額は、
V＝P(1＋nr)
よって、将来価額（V）を現価（P）に換算する計算式は、
P ＝ V /（1＋nr）＝V × 1 /（1＋nr）
1 /（1＋nr）が「現価表」のホフマン係数です。
この計算式をもとに、エクセルで「ホフマン係数表」を作成します。
法定利率（5％）の場合のホフマン係数表
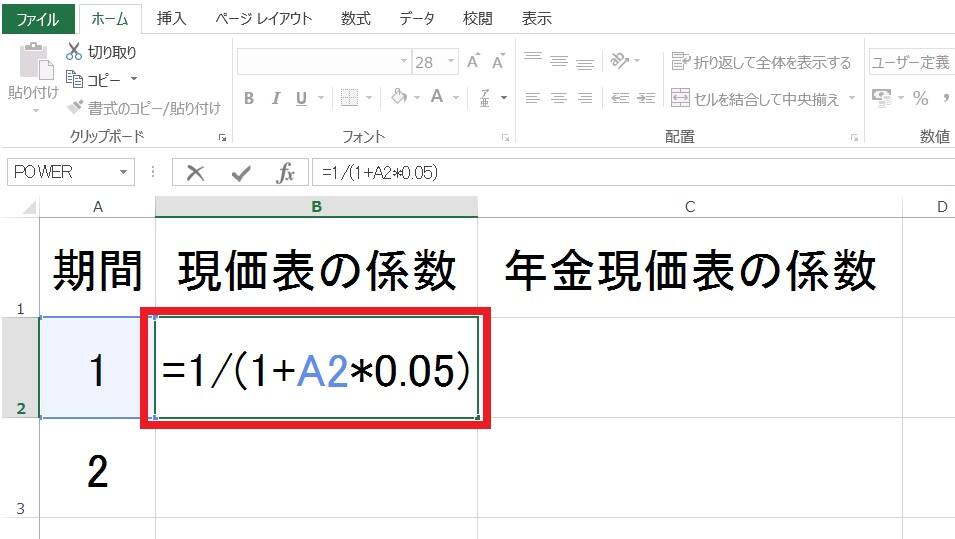
まず、「現価表」のホフマン係数の計算式を1年目のセルに設定します。
年利5％のホフマン係数は、
1 /（1＋nr）＝ 1 /（1＋n×0.05）
下の図のように計算式を設定します。あとは必要な年数分、計算式をコピペするだけです。
次に、「年金現価表」のホフマン係数です。1年目は「現価表」の係数と同じです。
「年金現価表」の係数は「現価表」の係数の年数分の積算ですから、2年目のセルに、1年目の「年金現価表」の係数と2年目の「現価表」の係数を加算する計算式を設定します。あとは同様に、必要な年数分をコピペです。
現価表のホフマン係数の計算式
年金現価表のホフマン係数の計算式
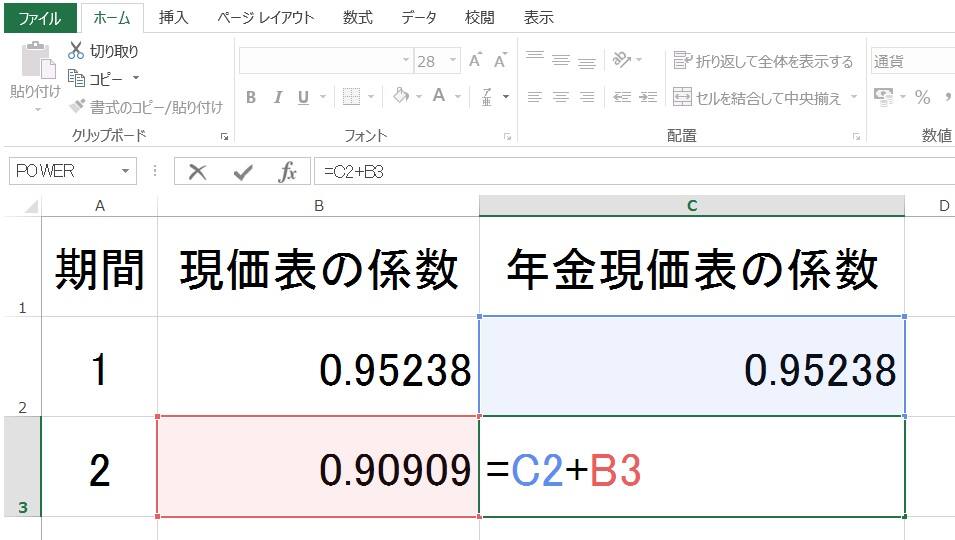
これで、ホフマン係数表（現価表・年金現価表）が作れます。
利率を3％で計算するなら「0.05」を「0.03」に変えればよいだけです。
ライプニッツ係数表（現価表・年金現価表）をエクセルで作る
ライプニッツ方式は、複利で運用することを前提に、将来の逸失利益を現在の価額（現価）に換算する方法です。別の言い方をすれば、複利で運用した場合の運用利息（中間利息）を控除して現価を出す方式です。
r：利率（年利）
n：期間（中間利息を控除する期間・年）
P：現在の価額（現価＝元本＝逸失利益）
V：将来の価額（n 年後の価額）
1年後の金額
「元本」に「1年間の利息」を加えた金額ですから、
P＋Pr＝P(1＋r)
ここは、単利計算の場合と同じですが、2年目以降が異なります。
2年後の金額
「1年後の金額」と「この1年間の利息」を加えた金額ですが、複利の場合は、元本と前年の利息を合計した金額（1年後の金額全体）に利息が付きます。
P(1＋r)＋P(1＋r)r＝P(1＋r)(1＋r)＝P(1＋r)²
3年後の金額
「2年後の金額」と「この1年間の利息」を加えた金額ですから、
P(1＋r)²＋P(1＋r)² r＝P(1＋r)² (1＋r)＝P(1＋r)³
n 年後の金額は、
V＝P(1＋r)^n
よって、将来価額（V）を現価（P）に換算する計算式は、
P ＝ V / (1＋r)^n＝V × 1 / (1＋r)^n
※「^n」は「n 乗」です。
1 / (1＋r)^n すなわち（1＋r）のn乗分の1 が「現価表」のライプニッツ係数です。
この計算式をもとに、エクセルで「ライプニッツ係数表」を作成します。
法定利率（5％）の場合のライプニッツ係数表
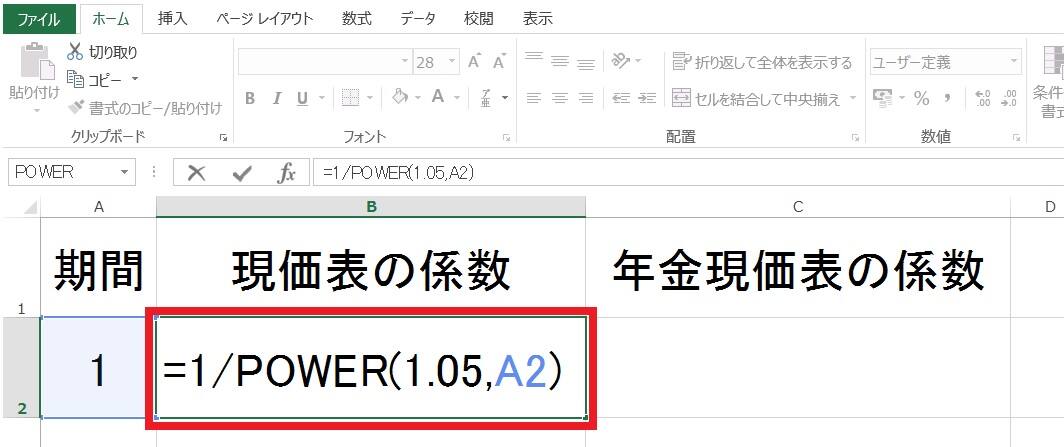
まず、「現価表」のライプニッツ係数の計算式を1年目のセルに設定します。
年利5％のライプニッツ係数は、
1 / (1＋r)^n ＝1 / (1＋0.05)^n ＝1 / (1.05)^n
下の図のようにPOWER（数値、指数）関数を用い、計算式を設定します。POWER関数は、数値を累乗した値を返します。あとは必要な年数分、計算式をコピペするだけです。
次に、「年金現価表」のライプニッツ係数です。1年目は「現価表」の係数と同じです。
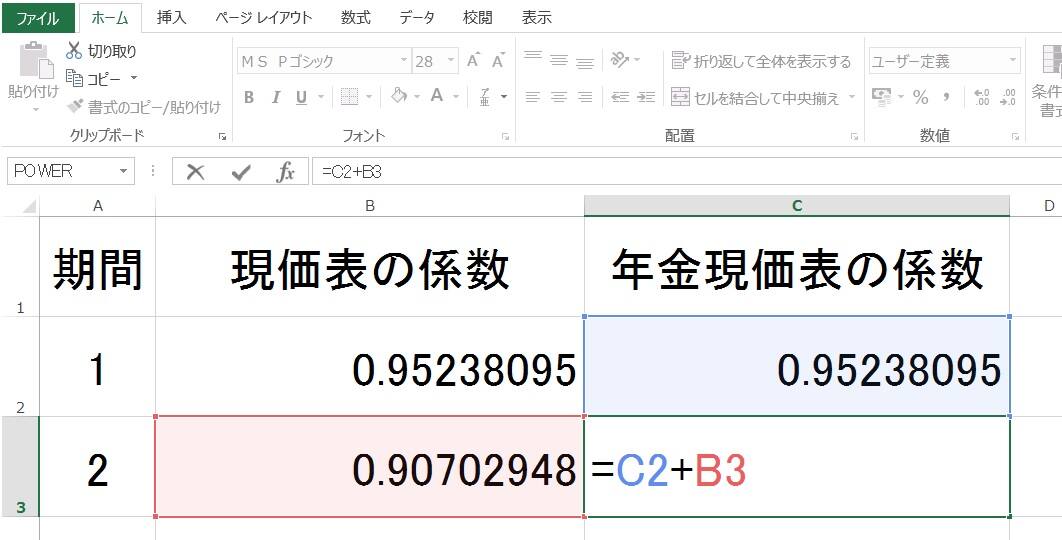
「年金現価表」の係数は「現価表」の係数の年数分の積算ですから、2年目のセルに、1年目の「年金現価表」の係数と2年目の「現価表」の係数を加算する計算式を設定します。あとは同様に、必要な年数分をコピペです。
現価表のライプニッツ係数の計算式
年金現価表のライプニッツ係数の計算式
これで、ライプニッツ係数表（現価表・年金現価表）が作れます。
利率を3％で計算するなら「1.05」を「1.03」に変えればよいだけです。
まとめ
ライプニッツ係数表やホフマン係数表は、エクセルを使って簡単に作成することができます。
ただし、もしも自分で逸失利益を計算して、保険会社と交渉しようと考えているのなら、ちょっと待ってください。交通事故の損害賠償請求は、定型化・定額化が進んでいますから、自分である程度は損害額を計算することはできます。
しかし、本当に満足できる損害賠償額を取得するには、やはり専門家の力が必要です。交通事故の損害賠償請求に強い弁護士に相談することをおすすめします。
弁護士に頼めば、あなたが本来受け取ることができる正当な損害賠償請求額を算定してもらえます。「えっ、こんなに賠償金をもらえるの?!」と驚かれることでしょう。保険会社とのやり取りで悩むこともありません。すべて弁護士に任せることができます。
弁護士に任せる方が、自分でいろいろ調べながら保険会社と交渉するより、結果的には納得できる解決ができるのです！
交通事故による被害・損害の相談は 弁護士法人・響 へ
弁護士法人・響は、交通事故被害者のサポートを得意とする弁護士事務所です。多くの交通事故被害者から選ばれ、相談実績 6万件以上。相談無料、着手金0円、全国対応です。
交通事故被害者からの相談は何度でも無料。依頼するかどうかは、相談してから考えて大丈夫です！
交通事故の被害者専用フリーダイヤル
0120-690-048 （ 24時間受付中！）
- 無料相談のお申込みは、こちらの専用ダイヤルが便利です。
- メールでも無料相談のお申込みができます。公式サイトの無料相談受付フォームをご利用ください。
※「加害者の方」や「物損のみ」の相談は受け付けていませんので、ご了承ください。
あなたにおすすめのページ
公開日 2017-04-18 更新日 2023/03/16 11:45:59
関連ページ
-
![]()
-
![]()
交通事故の被害者が18歳未満の場合、就労可能年数は18歳から67歳までの49年間ですが、適用するライプニッツ係数は、49年に対応するライプニッツ係数とは違いますから注意が必要です。 -
![]()
民法改正により法定利率が年5％から年3％に引き下げられ、3年ごとに1％刻みで見直す変動性が導入されました。年5％・4％・3％・2％の場合のライプニッツ係数・ホフマン係数を一覧でまとめています。 -
![]()
ホフマン方式で中間利息を控除する場合、中間利息控除期間（就労可能年数または労働能力喪失期間）が36年以上になると、賠償金元本から生じる年5％の利息が、年間の逸失利益を超える不合理が生じるといわれます。ホフマン係数の謎に迫ります。
