※当サイトでは記事内にアフィリエイト広告を含む場合があります。

ライプニッツ係数表・ホフマン係数表には、現価表と年金現価表があり、現価表と年金現価表は使うシーンが異なります。
ここでは、現価表と年金現価表の違い、それぞれどういう場面で使うのか、さらに、現価表と年金現価表の使い方について、見ていきます。
民法改正により法定利率が引き下げられ、2020年4月1日以降に発生した事故については新しい法定利率に対応するライプニッツ係数・ホフマン係数が適用されます。ここでは、年5%の法定利率のライプニッツ係数・ホフマン係数を用いています。
現価表と年金現価表の違い
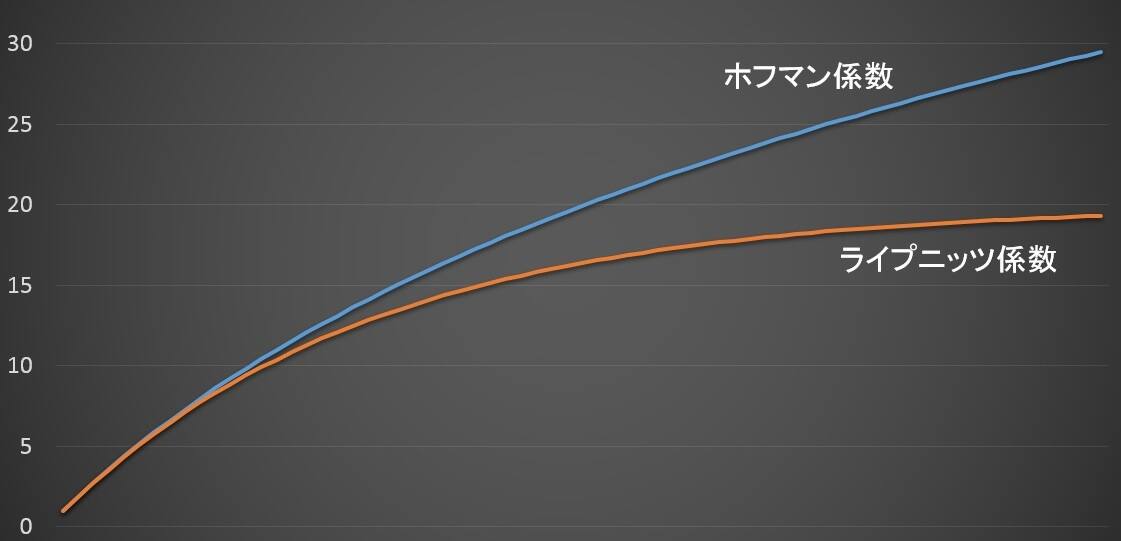
ライプニッツ係数・ホフマン係数は、逸失利益を計算する際に、中間利息を控除し、現在価額に換算するために用いる係数です。ライプニッツ係数は、中間利息を複利計算で控除し、ホフマン係数は、中間利息を単利計算で控除します。
現価表・年金現価表は、どんな場面で使うのか?
現価表と年金現価表は、それぞれ次のような場面で、将来受け取る価額を現在価額に換算するために使います。
| 現価表 |
将来入る一時金(●●年後に支払われる金額)を今すぐ受け取るとすれば、いくら受け取ることができるか、現価換算する場合に使用する係数を表にしたものです。 |
|---|---|
| 年金現価表 |
将来にわたって継続して入る収入(●●年間にわたり毎年支払われる金額)を今すぐ一時金で受け取るとすれば、いくら受け取ることができるか、現価換算する場合に使用する係数を表にしたものです。 |
現価表と年金現価表の関係
次の2つの表は、中間利息控除の利率が年5%のライプニッツ係数とホフマン係数を並べて記した現価表と年金現価表です。現価表と年金現価表の関係を見るため、5年分だけ抜粋しています。
現価表(年5%・年別・ライプニッツ係数・ホフマン係数)
| 年数 | ライプニッツ係数 | ホフマン係数 |
|---|---|---|
| 1 | 0.95238095 | 0.95238095 |
| 2 | 0.90702948 | 0.90909091 |
| 3 | 0.86383760 | 0.86956522 |
| 4 | 0.82270247 | 0.83333333 |
| 5 | 0.78352617 | 0.80000000 |
※5年分だけ抜粋
年金現価表(年5%・年別・ライプニッツ係数・ホフマン係数)
| 年数 | ライプニッツ係数 | ホフマン係数 |
|---|---|---|
| 1 | 0.95238095 | 0.95238095 |
| 2 | 1.85941043 | 1.86147186 |
| 3 | 2.72324803 | 2.73103708 |
| 4 | 3.54595050 | 3.56437041 |
| 5 | 4.32947667 | 4.36437041 |
※5年分だけ抜粋
年2~5%の各利率に対する70年分のライプニッツ係数とホフマン係数の現価表・年金現価表はこちらに掲載しています。
この表を見れば分かるように、年金現価表の係数は、現価表の係数を1年目から年数分足し合わせた数値です。
例えば、年金現価表で、年数が3年のライプニッツ係数は、現価表の1年から3年までのライプニッツ係数を足し合わせた数値です。ホフマン係数の現価表と年金現価表も、同様の関係があります。
実際に、上の現価表と年金現価表で確認してみてください。
年金現価表の2年のライプニッツ係数は、現価表の1年と2年のライプニッツ係数を足し合わせた数値です。
0.95238095+0.90702948=1.85941043
以下同様に、年金現価表の3年のライプニッツ係数は、現価表の1年~3年のライプニッツ係数を足し合わせた数値です。
0.95238095+0.90702948+0.86383760=2.72324803
このことは、年金現価表の係数の代わりに、現価表の係数を足し合わせれば、現価換算できることを意味します。このことは、あとで具体的な計算で説明します。
それでは、現価表と年金現価表の具体的な使い方を見ていきましょう。
現価表の使い方
次のようなケースを考えてみましょう。
5年後に支払われる100万円を、今すぐ受け取るとすれば、いくら受け取ることができるか?
こういうケースでは、現価表を使います。
現価表のライプニッツ係数を使って計算
5年に対応する現価表のライプニッツ係数は 0.78352617 です。100万円にこの係数を掛けます。
100万円×0.78352617=78万3,526円
こうして計算した78万3,526円が、5年後の100万円の現在価額です。
つまり、5年後に支払われる100万円を今すぐ受け取る場合は、78万3,526円に割り引いて支払われるということです。差額の21万6,474円は、中間利息として控除されます。
現価表のホフマン係数を使って計算
同様に、5年に対応する現価表のホフマン係数は 0.80000 です。100万円にこの係数を掛けます。
100万円×0.80000=80万円
こうして計算した80万円が、5年後の100万円の現在価額です。
つまり、5年後に支払われる100万円を今すぐ受け取る場合は、80万円に割り引いて支払われるということです。差額の20万円は、中間利息として控除されます。
中間利息を控除するのは、受け取った金額を元本として年利5%で運用すれば、5年後に100万円になるからですが、それを検証してみましょう。
ホフマン方式の場合で考えます。単利計算ですから、計算が簡単で中間利息控除のイメージがしやすいと思います。
受け取る金額80万円を元本として年利5%で5年間運用した場合の運用利息は、
80万円×0.05×5年=20万円
よって、元本と利息を合わせると
80万円+20万円=100万円
このように、年利5%で運用できれば、実際に5年後に100万円となります。
この式の利息20万円を左辺から右辺に移項すると
80万円=100万円-20万円
これが中間利息を控除することの意味です。
年金現価表の使い方
次のようなケースを考えてみましょう。
今後3年間、毎年100万円が入ってくる場合、合計300万円を今すぐ一時金で受け取るとすれば、いくら受け取ることができるか?
こういうケースでは、年金現価表を使います。
年金現価表のライプニッツ係数を使って計算
3年に対応する年金現価表のライプニッツ係数は 2.723248 です。100万円にこの係数を掛けます。
100万円×2.723248=272万3,248円
こうして計算した272万3,248円が、今後3年間に毎年100万円ずつ得られる合計300万円の現在価額です。
つまり、今後3年間にわたって毎年100万円が入ってくる場合、その合計300万円を一時金として今すぐ受け取るなら、中間利息として約28万円が控除され、およそ272万円に割り引いて支払われるということです。
年金現価表のホフマン係数を使って計算
3年に対応する年金現価表のホフマン係数は 2.731037 です。100万円にこの係数を掛けます。
100万円×2.731037=273万1,037円
こうして計算した273万1,037円が、今後3年間に毎年100万円ずつ得られる合計300万円の現在価額です。
つまり、今後3年間にわたって毎年100万円が入ってくる場合、その合計300万円を一時金として今すぐ受け取るなら、中間利息として約27万円が控除され、およそ273万円に割り引いて支払われるということです。
現価換算は、年金現価表を使わず現価表でも計算できる
現価換算は、年金現価表を使わず、現価表で計算できます。
現価表の係数は、1年ごとに現価を求める場合の係数ですから、現価表の係数を使って算出した現価を年数分足し合わせれば、年金現価表を使って計算した結果と同じになります。先に「現価表と年金現価表の関係」のところで説明したことを具体的な計算事例で見てみましょう。
上の「年金現価表の使い方」で示した事例と同じ事例で考えます。
今後3年間、毎年100万円が入ってくる場合、合計300万円を今すぐ一時金で受け取るとすれば、いくら受け取ることができるか?
ライプニッツ係数を使って計算
通常は年金現価表を使いますが、ここでは現価表のライプニッツ係数を使って、現在価額を計算します。
1年後に受け取る100万円の現在価額は
100万円×0.95238095=95万2,380.95円
2年後に受け取る100万円の現在価額は
100万円×0.90702948=90万7,029.48円
3年後に受け取る100万円の現在価額は
100万円×0.86383760=86万3,837.60円
よって、3年間毎年100万円ずつ受け取る合計300万円の現在価額は
95万2,380.95円+90万7,029.48円+86万3,887.60円=272万3,248.03円
上の「年金現価表の使い方」のところで示した3年に対応する年金現価表のライプニッツ係数により計算した現価と、現価表のライプニッツ係数により計算した各年の現価の3年分の合計が一致します。
3年間を足し合わせて、計算式を変形すると、次のようになります。
100万円×0.95238095+100万円×0.90702948+100万円×0.86383760
=100万円×(0.95238095+0.90702948+0.86383760)
=100万円×2.72324803
つまり、現価表のライプニッツ係数を1年から年数分足し合わせた数値が、年金現価表の年数に対応するライプニッツ係数となることが分かります。
ホフマン係数を使って計算
ホフマン係数を使う場合も、同様の結果となります。現価表のホフマン係数を使って、現在価額を計算します。
1年後に受け取る100万円の現在価額は
100万円×0.95238095=95万2,380.95円
2年後に受け取る100万円の現在価額は
100万円×0.90909091=90万9,090.91円
3年後に受け取る100万円の現在価額は
100万円×0.86956522=86万9,565.22円
よって、3年間毎年100万円ずつ受け取る合計300万円の現在価額は
95万2,380.95円+90万9,090.91円+86万9,565.22円=273万1,037.08円
3年に対応する年金現価表のホフマン係数により計算した現価と、現価表のホフマン係数により計算した各年の現価の3年分の合計が一致します。
3年間を足し合わせて、計算式を変形すると、次のようになります。
100万円×0.95238095+100万円×0.90909091+100万円×0.86956522
=100万円×(0.95238095+0.90909091+0.86956522)
=100万円×2.73103708
つまり、現価表のホフマン係数を1年から年数分足し合わせた数値が、年金現価表の年数に対応するホフマン係数となることが分かります。
まとめ
交通事故による逸失利益は、ライプニッツ係数やホフマン係数を用いて自分で計算することはできます。
しかし、逸失利益は、交通事故の損害賠償額の中でも大きな金額になるうえ、実際の逸失利益の計算には、高度な専門知識が必要です。交通事故に強い弁護士に相談することをおすすめします。
弁護士法人・響は、交通事故被害者のサポートを得意とする弁護士事務所です。多くの交通事故被害者から選ばれ、相談実績 6万件以上。相談無料、着手金0円、全国対応です。
交通事故被害者からの相談は何度でも無料。依頼するかどうかは、相談してから考えて大丈夫です!

 0120-690-048 ( 24時間受付中!)
0120-690-048 ( 24時間受付中!)
- 無料相談のお申込みは、こちらの専用ダイヤルが便利です。
- メールでも無料相談のお申込みができます。公式サイトの無料相談受付フォームをご利用ください。
※「加害者の方」や「物損のみ」の相談は受け付けていませんので、ご了承ください。